Computing Digits of π with CUDA

Ed Karrels, March 14, 2017

Happy pi day, 2017!

I'm finally posting the results of my last run, the 10 quadrillionth digit of pi. The initial computation took from January 8th to April 5th of 2014, and the doublecheck ran from April 9th to August 21. Each computation took about 90,000 hours of GPU time, or about 10 years, spread across 51 machines. Like the other runs, I'm only posting the first 8 digits I found, so I can hold back the other 17 in secret to verify other people's results. So far, nobody has taken me up on the challenge!

I've been taking a break in pi computations because I pretty much maximized the computation size that's practical with the computing resources I've got. Santa Clara University was very generous with their computer time and electric bills, but I've moved on to the University of Illinois, and here all the computing power is already in use working on much more practical projects. This would make a nice BOINC project. In the mean time, the code could use some cleaning up, and I'd like to optimize the CPU version of the code and port it to the Xeon Phi. Because in grad school, I've got a lot of spare time :-)

Here's a summary of my computations of π using CUDA:

Starting point Digits Completion Date Total time
 		GPU time
5 * 1014 + 64 8B223942697A609C4 2012-09-16 37 days 154 days
1 * 1015 8353CB3F7F0C9ACCFA9AA215F2 2012-10-24 39 days 297 days
2 * 1015 653728f1................. 2013-01-22 26 days 694 days
4 * 1015 5cc37dec................. 2013-05-20 32 days 1434 days
10 * 1015 9077e016................. 2014-04-05 88 days 3772 days

Happy pi day, 2014!

I'm still plugging away, currently working on computing the ten quadrillionth digit. It's been running for a couple months now, and at the current rate it should finish on tau day, June 28th (no, I didn't plan that). We had a little pi day party at the Santa Clara University campus and it made the local news.

If you're interested, I gave a presentation at the 2013 NVIDIA GPU Technology Conference. Here are my slides, and here is a video of the presentation either streaming or in downloadable FLV. Or you can find it here, under the title "Computing the Quadrillionth Digit of Pi: A Supercomputer in the Garage".

2013-05-23 Four Quadrillionth and counting...

After 32 days and 35,000 hours of GPU time (and another 32 days and 35,000 hours to doublecheck), my computation of the four quadrillionth digit of π has finished. Starting at the four quadrillionth hexadecimal digit of π, the next eight eigits are 5cc37dec .

I've computed another 17 digits after those, and again, I'll keep those under wraps to help confirm other people's computations.

2013-03-14 π day update: New Record!

To celebrate the 2013 π day, I'd like to announce a new record: the eight quadrillionth bit of π is 0!

OK, the odds of guessing that are pretty good, so how about more details?

Starting at the two quadrillionth hexadecimal digit (where each hexadecimal digit is four bits) the next eight digits of π are 653728f1.

All the computations were done on graphics cards rather than on regular CPUs. I spread the job across three sets of graphics card-enabled computers:

The initial run, targeting the 2,000,000,000,000,000th digit, took 35 days from December 19th to January 22nd. The doublecheck run, targeting the 2,000,000,000,000,008th digit, took 26 days from January 22nd to February 16th. The doublecheck run went faster because I used a newer version of the programming tools to build the program (CUDA compiler 5.0 versus 4.0).

The doublecheck run showed that 25 digits of the initial run were accurate. So I've got 25 new digits, but I'm only making the first eight public for now. That way, if and when someone else extends this result, I can help verify that they really did get accurate results in their computation.

I've been working on a program that uses CUDA to compute digits of π. CUDA is a programming system that lets you offload work from the main processor to the graphics card(s), which often have far more computing horsepower than the main processor. It started as a project for a course I took at Santa Clara University. On August 27th, I completed a run that set a new world record for the computation of π, and I intend to double that record within two months.

The previous record was set in 2011 by a team from Yahoo, and it was computed using a cluster of 1000 computers. I performed a similar computation, but starting a few decimal places further, on a single computer in my garage. All the processing was done on four NVIDIA GTX 690 graphics cards installed in that machine. Yahoo's run took 23 days; mine took 37 days.

With a theoretical peak throughput of 22.5 teraflops, this would have been one of the 100 fastest computers in the world five years ago.

Normally when computer and math geeks talk about computing π they're talking about computing every digit from the first decimal place to some target digit many decimal places later. The current record for that type of computation is 10 trillion digits, computed in 2011 by Alexander J. Yee and Shigeru Kondo.

In 1995 Bailey, Borwein and Plouffe discovered a new formula for π which makes it possible to compute a few digits of π without computing all the previous digits.

The Yahoo team used a variation on this formula to compute 64 hexadecimal (base-16) digits of π, starting at the 500 trillionth place: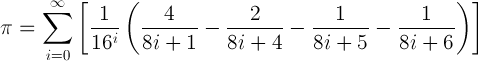 
    0E6C1294 AED40403 F56D2D76 4026265B
    CA98511D 0FCFFAA1 0F4D28B1 BB5392B8
My calculation started at the 500,000,000,000,056th place, overlapping the Yahoo results by eight digits (to doublecheck my results): 
    BB5392B8 8B223942 697A609C 45CD4228
Due to the nature of the computation, the last few digits of this result are bound to be inaccurate. I'm currently doing a second run, offset by four digits, to determine how many are accurate and thus by how much I have extended the record.

Update: Here are the results from the second run: 

  run 1:  BB5392B8 8B223942 697A609C 45CD4228                            
  run 2:      92B8 8B223942 697A609C 44D95A52FC3F
Seventeen of the new digits are correct. The final result, never computed before, is: starting at the 500,000,000,000,064th place, the next 17 hexadecimal digits of π are 8B223942697A609C4.

I'm going to make a few tweaks to the program, and then start a run twice as deep, starting at the one quadrillionth hexadecimal digit or four quadrillionth bit. The run should take about 40 days on my home machine. I'll be doublechecking the results simultaneously on a set of single-GPU computers at Santa Clara University.

Update 2012-10-24: The quadrillionth digit run finished! Here are the results: 

  353CB3F7 F0C9ACCF A9AA215F 2556D630
This doubles the previous record. My guess is that the first 24 digits are correct. I'm currently doing the doublechecking run, which should finish in about a week.

Update 2012-11-07: The results are good to 25 digits! Here are the results of the doublechecking run: 

  Initial run, starting at 1015+1: 353CB3F7 F0C9ACCF A9AA215F 2556D630
  Doublecheck, starting at 1015+5:     B3F7 F0C9ACCF A9AA215F 24E1CB4C7030
Update 2012-12-23: I thought it was awkward to know the quadrillion-and-first digit but not the quadrillionth, so I did a third run eight digits earlier: 
                                  quadrillionth digit
                                          |
                                          v
  Triplecheck, starting at 1015-7: 1C23D488 353CB3F7 F0C9ACCF A8262A4B
  Initial run, starting at 1015+1:          353CB3F7 F0C9ACCF A9AA215F 2556D630
  Doublecheck, starting at 1015+5:              B3F7 F0C9ACCF A9AA215F 24E1CB4C7030
So, the new record result is: starting at the 1,000,000,000,000,000th place, the next 26 hexadecimal digits of π are 8353CB3F7F0C9ACCFA9AA215F2.

After a couple months at a continuous draw of 1100 watts this power strip retired early.

Implementation Details

I used the Bellard formula in my program:
Each term is in the form 2A / (B i + C). Compute each of them separately: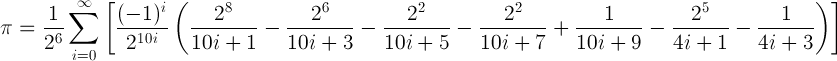
To start the computation at bit N, shift the result to the left by N bits by multiplying by 2N, and remove everything left of the decimal:

    (let D = A-6-10i+N)

    (let E = B i + C)

For these calculations, D and E are as large as 2 × 1014, which can be represented with a 64-bit integer but not a 32-bit integer. The main loop of the program is essentially: 
  for (i=...) {
    D = ...function of i...
    E = ...function of i...
    m = modularExponentiation(2, D, E);  // pow(2,D) % E
    total += m / E;
  }
Division is a slow operation, particularly on current NVIDIA GPUs, because they have no hardware division instruction. There is a single-precision floating point reciprocal instruction. For higher precision division, the compiler generates code that uses the reciprocal instruction and a series of Newton-Raphson approximations to achieve the desired precision. For a 32-bit integer divide, this results in 17 instructions. For 64 bits, 70 instructions.

The standard modular exponentiation algorithm uses many modulo operations, which are normally just as expensive as division operations. In my modular exponentiaion routine, I used Montgomery reduction to convert the modular base to a power of two, turning all the modulo operations into simple bitwise AND operations.

I used a 128-bit integer datatype to accumulate the results of the operation, so the division at each iteration of the main loop needed 128 bit of precison. Like the compiler-generated code, I used a few rounds of Newton-Raphson approximations to compute a high-precision reciprocal, then multiplied by the dividend.

GPU conference slides in Powerpoint and PDF.

Last updated 2013-3-14